Zeg je functionele gecijferdheid dan zeg je rekenen in de context van het dagelijks leven en beroep. Hoe laat je je leerlingen en studenten het beste kennismaken met de toepassing van hun rekenvaardigheden? Hoe kun je deze buitenwereld een goede plek in je lessen geven? Niet alleen dit soort toepassingscontexten kunnen je rekenonderwijs verrijken. In de verschillende leerfases kunnen ook ander soort contexten een ondersteunende rol spelen. In deze blog beschrijf ik hoe je contexten met kracht kunt inzetten in je rekenonderwijs.

Het gebruik van contexten heeft de potentie om de motivatie voor het rekenen te verhogen. Het geeft leerlingen en studenten een indruk van ‘waar je dat nu allemaal voor nodig hebt’. Maar motivatie is niet de enige reden om (meer) contexten aan het rekenonderwijs toe te voegen. Er zijn vele soorten contexten, met elk eigen doelen en eigen kenmerken. In deze blog wil ik twee daarvan uitlichten. Te beginnen bij het toepassen van rekenvaardigheden in authentieke situaties.
Rekenvaardigheden gebruiken in context
Meer dan de klassieke rekensom
Als je buiten het klaslokaal als volwassen burger je rekenvaardigheden gebruikt, dan merk je dat dit op een aantal punten verschilt van het rekenen zoals we dat klassiek binnen de muren van school ingericht hadden. De buitenwereld gedraagt zich nu eenmaal niet zo netjes als we dat in een gestileerde onderwijssetting graag zouden willen. We zien overal procenten, maar heel vaak is niet duidelijk wat ‘de 100%’ in die context is. Op de markt koop je een kilo kaas in plaats van een kilogram. En heel vaak mist een deel van de informatie waarmee je zou willen rekenen. Om maar eens een paar voorbeelden te noemen.
Het verschil is niet alleen dat het dagelijks rekenen wat rommeliger verloopt. Steeds vaker zijn de berekeningen namelijk al voor ons uitgevoerd. We moeten dan vooral betekenis geven aan de uitkomst van die berekening. In de supermarkt bijvoorbeeld zijn de prijzen per liter, per kg of per stuk als voor ons uitgerekend. Dat maakt het vergelijken van producten eenvoudig. Althans dat zou je denken. De prijs per eenheid product is echter niet altijd de juiste vergelijkingsmaat. Denk maar eens aan die reclames van een bekend afwasmiddel: zij lieten zien dat één fles van hun merk qua afwaskracht gelijk stond aan wel drie flessen van de concurrent. De sterkere concentratie maakt dit afwasmiddel uiteindelijk goedkoper per afwasbeurt. Het is een mooi voorbeeld waarom kritisch denken steeds belangrijker wordt.
Rekenhulpmiddelen
Er is nog een ander belangrijk verschil: rekenhulpmiddelen. Dit zijn echte gamechangers. Je hoeft maar je telefoon op een rekensom te richten en met de juiste app krijg je het antwoord, een uitwerking en soms zelfs uitleg hoe je iets moet aanpakken. Maar niet alleen wordt het rekenen steeds vaker overgenomen. Interessant is dat er ook andere manieren van rekenen handiger worden. Dit heeft invloed op hoe we onze doorgaande leerlijn in kunnen richten.
Bijvoorbeeld bij het berekenen van de prijs per liter. Stel dat een fles limonade van 0,6 liter een prijs heeft van € 3,99. Waar we zonder rekenmachine handige tussenstappen kozen om het rekenen eenvoudig te houden, is dat zonder rekenmachine niet nodig. Zonder rekenmachine is het handig om via 0,2 liter te rekenen. € 3,99 ÷ 3 = € 1,33. Een liter kost dus € 1,33 × 5 = € 6,65. Op de rekenmachine kun je in één keer € 3,99 ÷ 0,6 uitrekenen. Hierbij gebruik je het inzicht dat als je de prijs van 5 liter weet, je door 5 deelt voor de literprijs. Weet je de prijs van 2,5 liter, dan deel je door 2,5 en als je de prijs van 0,6 liter weet, deel je door 0,6 om de literprijs te berekenen. Deze aanpak staat trouwens haaks op de strategie om eerst uit te rekenen hoeveel 1 ml kost en dan te rekenen naar de prijs per liter. Een strategie die ook mogelijk is geworden door de rekenmachine, maar minder efficiënt is.
De voorbeelden laten zien dat rekenen in het dagelijks leven naast de ’technische rekenvaardigheden’ vraagt om het begrijpen van de context, het herkennen van rekenen in je omgeving, zelfvertrouwen en hogere denkvaardigheden zoals kritisch denken en probleemaanpak (zie ook het Common European Numeracy Framework).
Rekenen in andere disciplines
Bij het toepassen van je rekenvaardigheden hoort ook het gebruik ervan in andere disciplines. Om hier meer zicht op te krijgen is het interessant om naar de eindexamens1 te kijken. Bijvoorbeeld deze opgave uit het GT biologie examen (2022 1e tijdvak).
Leven met diabetes
Jarno heeft de ziekte diabetes type 1, Zijn eilandjes van Langerhans maken geen insuline. Jarno houdt bij hoeveel koolhydraten hij eet en berekent dan hoeveel insuline hij moet inspuiten. Voor elke 8 gram koolhydraten die hij eet, moet Jarno 1 eenheid insuline inspuiten.
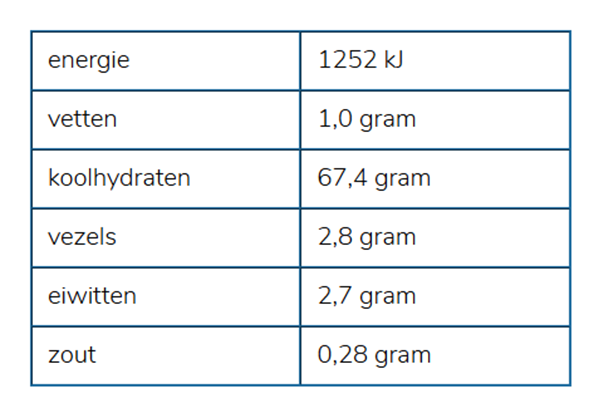
Jarno neemt als tussendoortje een plak ontbijtkoek van 70 gram. In de tabel zie je de voedingswaarde van ontbijtkoek per 100 gram.
Hoeveel eenheden insuline moet Jarno inspuiten na het eten van zijn tussendoortje?
De eerste stap is het uitrekenen van het aantal koolhydraten in de plak ontbijtkoek. Hier kun je op verschillende manieren tegenaan kijken. In mijn steekproef onder mijn publiek wordt er het meest gerekend met 0,7 × 67,4. Je gaat dan uit van 70/100 deel van de hoeveelheid per 100 gram. De tweede stap in deze opgave is om hierbij het aantal eenheden insuline uit te rekenen. Daarin ligt meer eensgezindheid in mijn publiek. Bijna iedereen rekent dit uit door het aantal koolhydraten door 8 te delen.
Het interessante van dit voorbeeld is dat er twee soorten verhoudingen naar voren komen: een interne- en externe verhouding (hier vind je daarover een uitgebreide uitleg). Het laat daarmee zien dat voor het rekenen met verhoudingen een bepaalde flexibiliteit erg belangrijk is. Ook zie je hier dat, in ieder geval mijn publiek dit soort berekeningen op een intuïtieve manier, maar wel op formeel niveau uitvoert. Deze eigen voorkeur is niet altijd hetzelfde als de rekenstrategie die aan leerlingen en studenten wordt aangeleerd.
Bovenstaande laat zien dat om in het dagelijks leven te kunnen rekenen, je meer nodig hebt dan alleen een procedurele beheersing van ’technische rekenvaardigheden’. Conceptueel begrip van de onderliggende structuren, de ambiguïteit en de samenhang2 van de rekenonderwerpen uit het curriculum is nodig om op een hoger beheersingsniveau te rekenen en om betekenis te geven aan de uitkomsten. Begrijpen wat je aan het doen bent, helpt bovendien problemen aan te pakken die afwijken van de standaard.
Concreet beginnen met contexten
Emergent modelleren
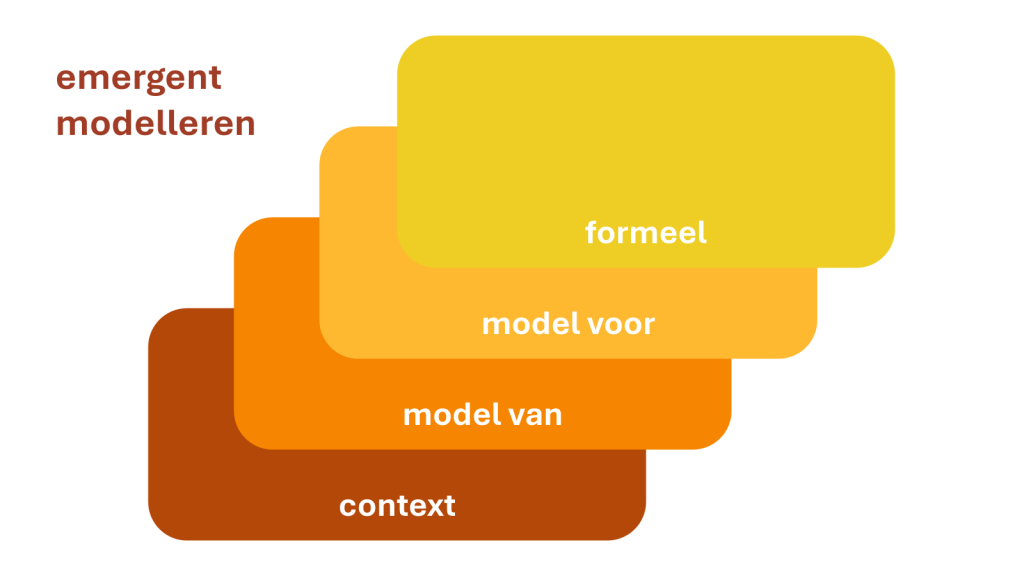
Om dat conceptuele begrip te bevorderen kan een ander soort context gebruikt worden in de rekenles. Welke didactiek je ook gebruikt, nooit start het leren van rekenen-wiskunde op abstract niveau. Het gebruik van een context verlaagt de drempel en maakt het denken over rekenen-wiskunde makkelijker. Je ziet dit in allerlei modellen terug, zoals in het handelingsmodel uit het ERWD protocol. Zelf vind ik de taal van een wat ouder model behulpzaam bij het nadenken over contexten en rekenmodellen: emergent modelleren3.
Het doel van de te ontwerpen leerroute is om uiteindelijk op formeel niveau uit te komen. De stappen staan daarvan in dienst. Als docent zoek je daarom een ‘context’ die qua structuur past bij het rekenen-wiskunde waar je op formeel niveau naartoe wilt werken. Deze context moet daarbij voorstelbaar voor leerlingen en studenten zijn. Je noemt dat realistisch. Dit betekent niet dat de context authentiek is zoals bij de toepassingsopgaven. Bij authentieke contexten zorgt de werkelijkheid juist voor extra inconsistenties en ruis. Een realistische context moet juist dergelijke ruis vermijden. Dat betekent dat de contexten soms wat gezochter aan kunnen voelen. Zo’n context wordt dan aan leerlingen/studenten geïntroduceerd, vaak met concreet materiaal. In het gesprek met elkaar ontstaat op een gegeven moment de behoefte om de context te schematiseren; er ontstaat een ‘model van’ de context. Dit model ontwikkelt zich geleidelijk in een ‘model voor’ rekenkundig redeneren. Na verloop van tijd kan de leerling/student dit model loslaten om op ‘formeel’ niveau te rekenen. Het idee achter deze opbouw is dat een leerling/student altijd terug kan vallen op het begrip van een onderliggend niveau wanneer het formele niveau even uit het zicht is.
Het model van emergent modelleren laat zien dat een context effectief is als …
- … deze eenzelfde structuur ondersteunt als op het formele niveau nodig is
- … deze voor de lerende voorstelbaar is (realistisch)
- … deze géén kenmerken heeft die ruis kunnen veroorzaken
Een model of schematisering is effectief als …
- … deze aansluit bij de gekozen context
- … deze van de leerling zelf is
- … deze het rekenkundig redeneren stimuleert
- … je deze los kunt laten
- … je er altijd op terug kunt vallen
De valkuil van modellen
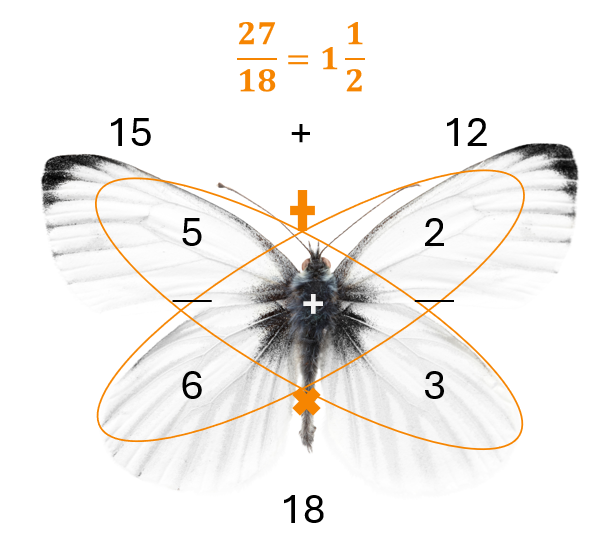
Schematiseringen en modellen worden veel gebruikt in het rekenonderwijs. Toch voldoen ze niet allemaal aan bovenstaande lijstje. Tijdens lesobservaties zie ik met regelmaat leerlingen/studenten die moeite hebben om ‘de som te vertalen naar het schema’. Staan de getallen eenmaal in het schema dan lukt het wel om tot een antwoord te komen. Het is een symptoom van modellen en schema’s die geen betekenis meer hebben, die het begrip van de rekenvaardigheid niet ondersteunen. Een bekend voorbeeld is de vlinder om breuken op te tellen4.
De vlinder is niets meer of minder dan een visuele reminder voor een bepaald stappenplan. Het model is populair omdat je er snel effect mee kunt bereiken. Binnen een lesuur kun je op deze manier leerlingen breuken leren optellen. Er kleven veel nadelen aan dit soort visuele reminders door het gebrek aan begrip van wat je aan het doen bent:
- De retentie van deze modellen is slecht. Op de langere termijn ontstaan er eenvoudig varianten die tot een verkeerd antwoord leiden.
- Het model is beperkt toepasbaar en daarom is de transfer laag. Bovenstaand model kan immers niet zomaar gebruikt worden om 3 breuken op te tellen.
- De manier van rekenen is vaak efficiënt. In het voorbeeld was het eenvoudiger om 5/6 + 4/6 als tussenstap te nemen.
- Het is lastig om vanuit deze modellen naar het formele niveau door te groeien.
- Dergelijke modellen bieden géén basis voor vervolgonderwerpen binnen het rekenen.
De modellen die we in het Nederlandse onderwijs gebruiken hebben op zichzelf niet deze kenmerken. Toch zie ik in het gebruik ervan dat ze verworden tot juist alleen maar zo’n visuele reminder. Ze worden dan dogmatisch in het gebruik en daardoor verliest het model veel van zijn kracht.
Context en taal
Heel vaak wordt het rekenonderwijs te talig genoemd. De toetsing wordt dan gezien als een test in begrijpend lezen in plaats van het laten zien van rekenvaardigheden. Het is jammer als daaruit de conclusie wordt getrokken dat je contexten moet weren uit je rekenonderwijs of ze pas aan het einde moet introduceren. In het algemeen is taal essentieel bij het leren. Juist als je iets verwoordt, helpt dat je begrijpen. In de rekenles is dat niet anders. De contexten die ik in deze blog heb beschreven kenmerken zich door rijke taal.
Realistische contexten aan het begin van het leerproces worden vaak mondeling en met objecten geïntroduceerd. Het is dan altijd mogelijk om taal aan te vullen waar iets niet duidelijk is. Datzelfde geldt ook als je over de toepassing van rekenvaardigheden praat met leerlingen en studenten. Het verschil in taal is dat aan het begin van het leerproces ontwikkeling van rekentaal een meer prominente rol in zal nemen.
Krachtige contexten
In deze blog heb ik je twee soorten contexten laten zien die in het rekenonderwijs een rol spelen. Ik hoop daarmee te hebben laten zien hoe deze contexten kunnen motiveren, hoe ze drempels kunnen verlagen en hoe ze ruimte kunnen geven voor het met begrip leren rekenen en zelf nadenken. Hoe een context eruit ziet en aan welke kenmerken deze moet voldoen om optimaal te kunnen worden gebruikt, hangt af van het doel dat je op dat moment nastreeft. Het is een aanrader om daarbij het verschil tussen realistische en authentieke contexten scherp in de gaten te houden.
Deze blog is een vrije weergave van de keynote die ik mocht geven op het Rekenfestival van ROC van Amsterdam-Flevoland op 8 april 2025.
1: Voor Studyflow heb ik Rekenen op je examen ontwikkeld, waarmee leerlingen hun rekenvaardigheden leren toepassen in 6 examenvakken. Dit voorbeeld is opgenomen in die methode.
2: De termen structuur, samenhang en ambiguïteit worden uitgelegd in het boek Mijn vakdidactiek.
3: Emergent modelleren komt uit het werk van Koeno Gravemeijer: How emergent models may foster the constitution of formal mathematics
4: Dit voorbeeld wordt uitgelegd door Phil Daro in zijn lezing: Against answer getting.