Gisteren organiseerde KPZ het rekendiner in Zwolle. Een heerlijke bijeenkomst voor rekencoördinatoren. Met als thema meten en meetkunde was het programma gevuld. Hoewel meetkunde er soms wat karig vanaf komt in het curriculum, liggen er in dit onderwerp mooie kansen om met de leerlingen aan de slag te gaan. In deze blog vind je een kort verslag en voor de deelnemers heb ik de plaatjes opgenomen die misschien wat te kort in beeld waren.

In mijn bijdrage nam ik de deelnemers mee langs meetkundige onderwerpen die ik zelf zo mooi vind. Daarmee probeerde ik een aantal dingen te laten zien:

• Het belang van het leren kijken.
• Het leren dat er vele verschillende manieren zijn om tot een oplossing te komen.
• Niet alleen de verschillende perspectieven erkennen, maar ook de relatie leggen tussen de perspectieven is van grote meerwaarde.
• Het veranderen van socio-math norms: het gaat niet altijd om het cijfermatige antwoord.
• Kennismaken met het generaliseren: op zoek naar algemeen geldende regels en patronen.
• Loskomen van stappenplannen en in plaats daarvan ervaring opdoen met oplosheuristieken.
• De kracht van het visuele ontdekken, zowel als visueel bewijs als ondersteuning van een redenering.

Ik begon met de fascinatie voor al die verschillende bewijzen voor de stelling van Pythagoras die al in mijn tienerjaren ontstond. Het idee dat er vanuit zoveel verschillende perspectieven kon worden gekeken vond ik destijds een eye-opener.

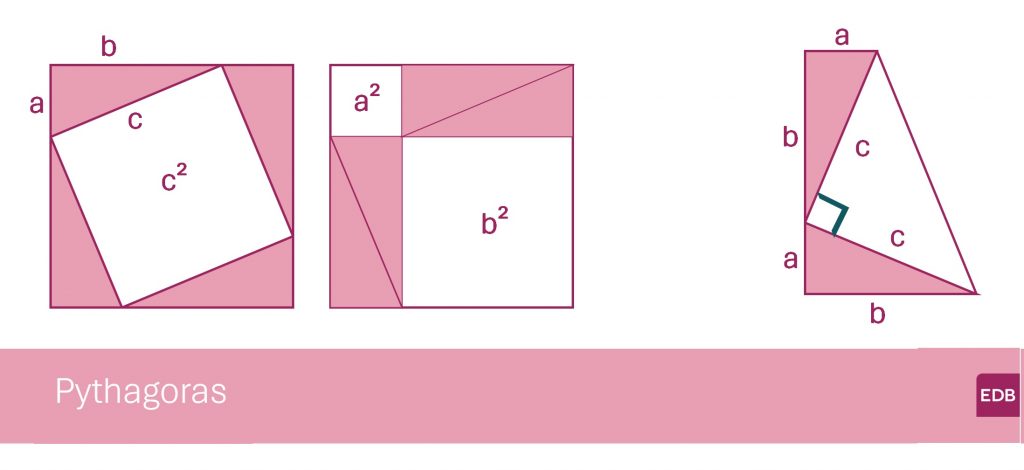
Hier vind je twee van die bewijzen. Het bewijs links is misschien wel de bekendste. De oppervlakte van de grote vierkanten is gelijk: c² + 4 driehoeken of a² + b² + 4 driehoeken. Rechts een wat minder bekend bewijs. Je kunt de oppervlakte van dit trapezium op twee manieren uitrekenen: met de formule voor de oppervlakte van het trapezium (1/2 × hoogte × (basis 1 + basis 2)) of als de oppervlakte van de losse driehoeken.

Vanuit deze stelling gingen we verder naar het bepalen van de oppervlakte van bepaalde figuren. Daarmee kon ik laten zien dat het niet altijd om de getallen hoeft te gaan. Het gesprek ging hier vooral over het kijken: hoe is het gekleurde vlak waarvan je de oppervlakte wilt uitrekenen opgebouwd uit vlakken waarvan je de oppervlakte eenvoudig kunt uitrekenen. Onder makkelijk uitrekenen verstonden we rechthoek, cirkel en driehoek. Ook hier liet ik verschillende figuren zien.

Tip: als je dit leuk vindt, dan zijn er heel veel voorbeelden te vinden op Pinterest.

Bij het plaatje links kun je de oppervlakte op uitrekenen als de oppervlakte van de rechthoek min de oppervlakte van de twee cirkels. Het resultaat deel je dan door twee. Een andere manier om hiernaar te kijken is door een verticale hulplijn tussen de twee cirkels te tekenen. Nu kun je de twee roze stukjes links van de hulplijn precies naar de rechterkant van de figuur verplaatsen. Dan zie je dat de roze stukken samen een vierkant min één cirkel vormen.

Bij de rechterfiguur waren er nog meer mogelijkheden. Deze heb ik hieronder samengevat:

Via wat visuele bewijzen en de uitleg hoe je kunt laten zien dat voor alle driehoeken geldt dat de oppervlakte 1/2 × basis × hoogte is, kwamen we bij het slotonderwerp uit. Ik ben namelijk gek op geometrische patronen of ook wel ‘behangpatronen’ genoemd. Het is sowieso leuk om met elkaar te zoeken wat de punten voor draaisymmetrie zijn en wat de orde van symmetrie daar is. (De orde is het aantal keren dat het figuur ‘op zichzelf’ valt als je een hele draai maakt van 360 graden). Als je echter weet dat er maar 17 verschillende structuren zijn (wiskundig bewezen) dan helpt je dat enorm bij het vinden van die punten voor draaisymmetrie. Je zoekt daarvoor naar een soort hoofdstructuren. Bijvoorbeeld van vierkanten of zeshoeken:

Tip: Al een tijd lang verzamel ik mooie patronen en plaats daar dan een blog over. In mijn post Behangpatronen vind je een lijstje met al de posts over dit onderwerp. Zo vind je een aantal mooie patronen waarmee je je eigen kijkvaardigheden kunt testen en oefenen.